Transformer位置编码的理解。
transformer原始位置编码
公式
更好的捕捉短距离和长距离的依赖关系
该控制通过改变$\frac{pos}{10000^{2i/d_{\text{model}}}}$ 来控制正弦或余弦函数的频率,可以很好捕捉短距离和长距离的依赖关系,位置编码可视图见下图:
- 短距离依赖关系(序列中相邻元素或位置之间的关系):低维频率较高,能够很好地捕捉到相邻位置之间的细微变化,可以区别短距离的位置。
- 长距离依赖关系(序列中相隔较远的元素或位置之间的关系):高维频率较低,能够很好地捕捉到较远维度之间的细微变化,可以区别长距离的位置。
当 2i 接近 $d_{model}$ 时,分母接近 10000,此时周期为 $10000*2π$
类别二进制中低维数值和高维数值的变化情况:
让我们打印出0, 1, 2, …, 7 的二进制表示形式。 正如所看到的,每个数字、每两个数字和每四个数字上的比特值 在第一个最低位、第二个最低位和第三个最低位上分别交替。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20for i in range(8):
print(f'{i}的二进制是:{i:>03b}')
# Output:
# 0的二进制是:000
# 1的二进制是:001
# 2的二进制是:010
# 3的二进制是:011
# 4的二进制是:100
# 5的二进制是:101
# 6的二进制是:110
# 7的二进制是:111
每个位置(pos)都是唯一的
因为维度很高时,周期很大,所以,每个位置的 pos必定是唯一的。
再加上低维不同频率的复杂组合,使位置编码包含丰富的位置信息。
为什么交错使用sin 和cos,而不能直接用其中有一个
对于原始交错情况:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19import matplotlib.pyplot as plt
import numpy as np
pos = np.arange(0, 100)
d_model = 20
PE_sin = np.sin(pos[:, np.newaxis] / 10000**(2 * np.arange(d_model // 2) / d_model))
PE_cos = np.cos(pos[:, np.newaxis] / 10000**(2 * np.arange(d_model // 2) / d_model))
PE = np.empty((pos.size, d_model))
PE[:, 0::2] = PE_sin
PE[:, 1::2] = PE_cos
plt.figure(figsize=(10, 8))
plt.imshow(PE, aspect='auto', cmap='viridis')
plt.colorbar()
plt.title('Positional Encoding (Sin and Cos)')
plt.xlabel('Encoding Dimension')
plt.ylabel('Position')
plt.show()
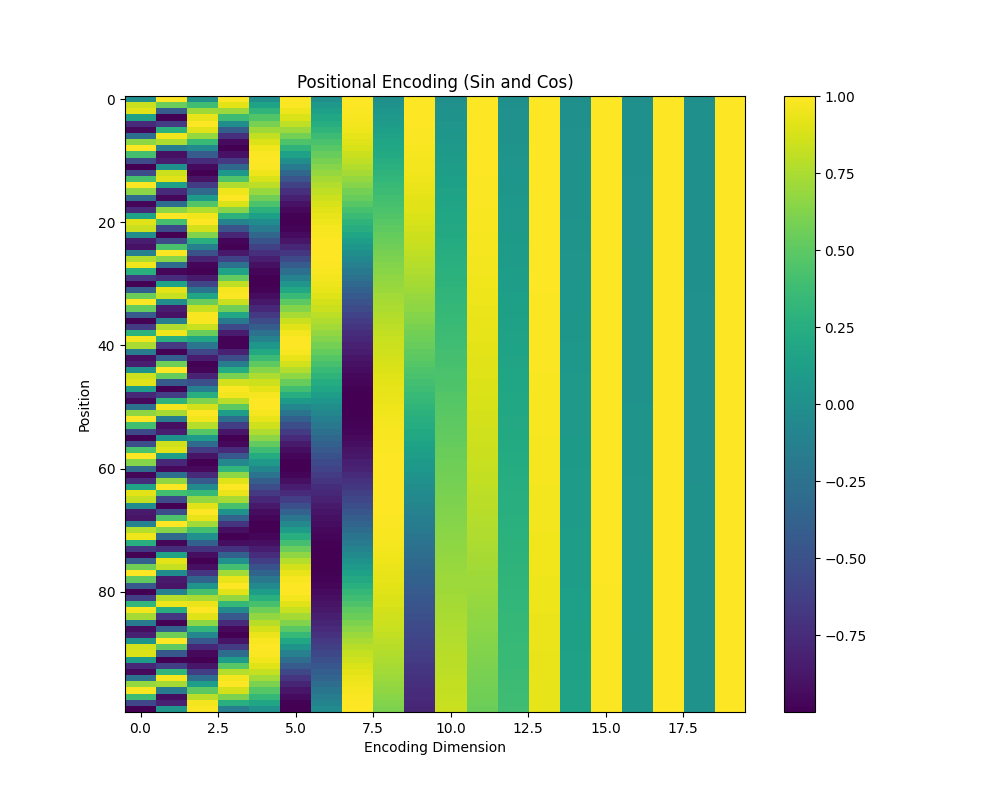
可以看到,对于某一行(某一个位置)来说,相邻维度的区别会非常明显,有利于模型区别各个维度,这是因为 sin与 cos相差一个$𝜋/2$ 个相位,在同一个位置会生成不同的值。
若只用 sin的话,如下图所示:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17import matplotlib.pyplot as plt
import numpy as np
pos = np.arange(0, 100)
d_model = 20
PE_sin = np.sin(pos[:, np.newaxis] / 10000**(np.arange(d_model) / d_model))
PE = np.empty((pos.size, d_model))
PE[:, :] = PE_sin
plt.figure(figsize=(10, 8))
plt.imshow(PE, aspect='auto', cmap='viridis')
plt.colorbar()
plt.title('Positional Encoding (Sin and Cos)')
plt.xlabel('Encoding Dimension')
plt.ylabel('Position')
plt.show()
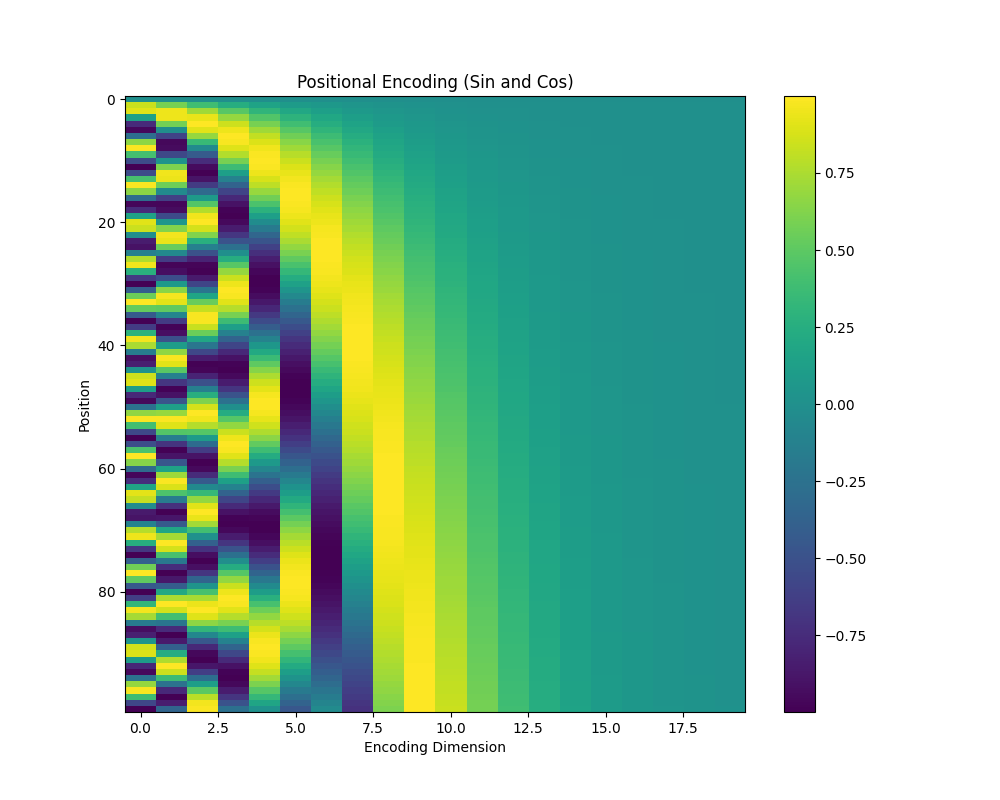
对于高维,相邻位置区分较差。
另外的好处是:sin 和 cos函数在数学上是正交的,即它们在一个周期内的内积为零。这种正交性确保了它们在不同维度上的表示是独立的,可以更好地捕捉到不同位置的特征。
证明sin 和 cos函数在数学上是正交的:
No match found for heading: #证明 $ sin(x)$ 和 $ cos(x)$ 在数学上是正交的
相对位置编码
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移 $\delta$,位置 $i + \delta$ 处的位置编码可以线性投影位置 $i$ 处的位置编码来表示。
这种投影的数学解释是,令 $\omega_j = \frac{1}{10000^{2j/d}}$,对于任何确定的位置偏移 $\delta$,任何一对 $(p_{i,2j}, p_{i,2j+1})$ 都可以线性投影到 $(p_{i+\delta,2j}, p_{i+\delta,2j+1})$:
上面, $(p_{i,2j}, p_{i,2j+1})$ 其实可看作是坐标系中圆上的一点,而$(p_{i+\delta,2j}, p_{i+\delta,2j+1})$ 是相位相差$\delta$ 的圆上的另一点,在相同列 (同一维度)上,$(p_{i,2j}, p_{i,2j+1})$ 这些点在同一圆上,只是相位不同。
上面的矩阵,为旋转矩阵。
总结
正余弦位置编码的设计 很可能来源于 傅里叶变换。