0%

DBNet详解

发表于 分类于 阅读次数： Valine：
本文字数： 6.3k 阅读时长 ≈ 10 分钟

DBNet论文解读。

简介

全称：Differentiable Binarization
主要贡献：提出了 可微的、使二值化过程可训练的 DB模块。
key idea: 用 $Softmax$ 代替 简单粗暴 二极值化 $\Rightarrow$ 可导
DB模块联合一个简单的分割网络，得到了一个鲁棒的、快速的文字检测器。
优点：

  1. 精度高：水平、多向、弯曲文字。
  2. 更快：简化了后处理。
  3. 在轻量网络（resnet-18）上表现很好。
  4. DB模块在推理中可以去掉。

网络结构


box formulation module？
应该就是求连通域的计算。

概率图、阈值图、二值图 的shape与原图一样，因为在图中的pred阶段，进行了两次转置矩阵操作，每次都上采样 2 倍（stride=2）

负标签的loss为什么长这个样子，为什么与正标签的 loss不同？

精度变高的原因：
二值化：$\frac{1}{1 + e^{-t}}$，$K = 50$ $\Rightarrow$ 增强 $loss$ 效果

经典的二分类的交叉熵损失

经典的二分类的交叉熵损失中，一般不是负样本因为 label为 0，都被省略了吗？

你提到的情况是部分正确的，但省略负样本的说法可能有些误解。我们来详细解释一下二分类问题中的交叉熵损失是如何计算的。

在二分类问题中，对于每个样本，我们有一个标签 $y$，其值为 0 或 1。模型输出的预测概率为 $\hat{y}$，表示预测为正类的概率。交叉熵损失通常定义为：

这个公式包含了两个部分：

  1. 正样本 ($y = 1$)：

    • 当 $y = 1$ 时，损失为：这个部分是我们希望最大化的，表示模型正确预测正样本的概率。

  2. 负样本 ($y = 0$)：

    • 当 $y = 0$ 时，损失为：这个部分是我们希望最小化的，表示模型正确预测负样本的概率（即输出接近0）。

因此，负样本的损失是不会被省略的，只是因为当 $y = 0$ 时，第一个项 $y \cdot \log(\hat{y})$ 为 0，被省略的是正样本的损失项（因为它不贡献于此）。

在实际实现时，如果我们专注于正样本（例如在一些特定应用场景下），有时候我们会只计算正样本的损失。但是在标准的二分类交叉熵损失计算中，负样本的损失也是被明确计算的，用来确保模型能够正确识别负样本。这与前面讨论的公式一致，只不过两者的表达形式稍有不同。

正样本和负样本损失函数的求导过程详细说明

正样本导数：

负样本导数：

在这部分中，我们会推导正样本和负样本损失函数的导数。

1. 正样本损失函数 $l^+$

首先，正样本的损失函数 $l^+$ 被定义为：

这里的 $x = P_{i,j} - T_{i,j}$，其中 $P_{i,j}$ 是预测的概率值，$T_{i,j}$ 是阈值。首先，我们需要对这个函数进行化简。

可以将这个损失函数进一步简化为：

然后，我们对 $l^+$ 对 $x$ 求导：

使用链式法则来求导：

进一步对 $e^{-kx}$ 求导：

因此，最终的导数为：

我们注意到 $ \frac{1}{1 + e^{-kx}}$ 实际上就是函数 $f(x)$ 的定义：

因此，正样本损失函数的导数可以表示为：

2. 负样本损失函数 $l^-$

接下来，我们考虑负样本的损失函数 $l^-$，它被定义为：

首先，我们对括号中的表达式进行化简：

化简后，负样本的损失函数可以写成：

现在对 $l^-$ 对 $x$ 求导：

注意到 $f(x)$ 是 $\frac{1}{1 + e^{-kx}}$，所以可以进一步简化为：

所以，负样本损失函数的导数为：

总结

  • 对于正样本损失函数 $l^+$，导数为：

  • 对于负样本损失函数 $l^-$，导数为：

这两个导数公式帮助我们理解在可微分二值化中的梯度更新方式。正样本和负样本的梯度更新通过放大因子 $k$ 进行调节，优化时对错误预测的区域进行更显著的调整。

Deformable convolution

  • 可变形卷积 对 文字这种极端的长宽比有益


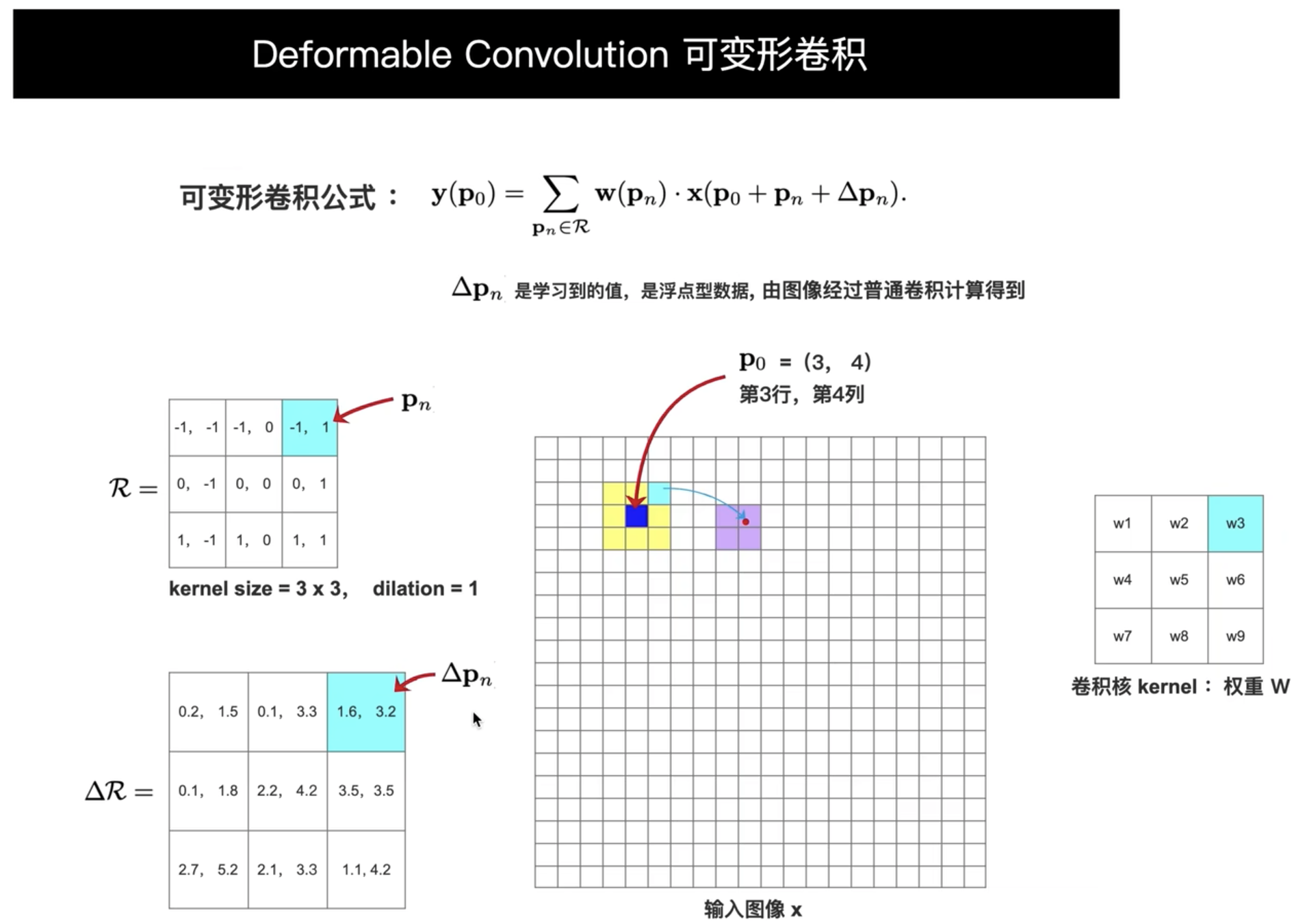
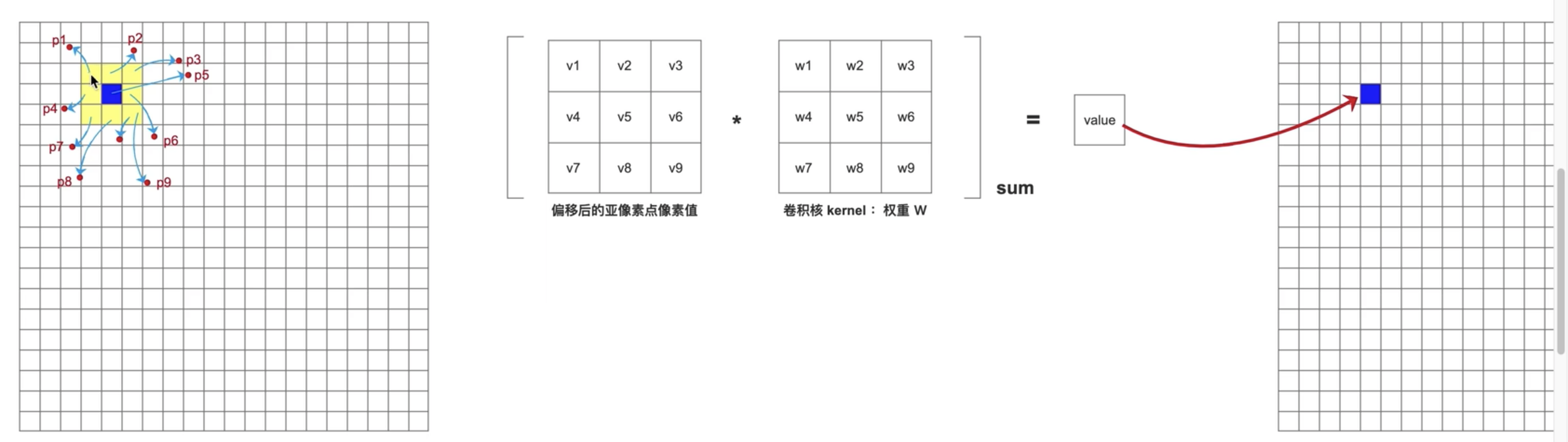
优势与应用

  • 适应性: 可变形卷积能够根据输入内容调整卷积核的位置，因此在处理具有较大变形的对象时，表现更好。
  • 提高检测精度: 在目标检测、语义分割等任务中引入可变形卷积，可以显著提高模型的检测精度，尤其是在处理形变多样的对象时。
  • 广泛应用: 可变形卷积在各种计算机视觉任务中得到了广泛应用，如目标检测（Deformable R-CNN）、语义分割（Deeplab系列）等。

实际效果

在实际应用中，可变形卷积能够有效提升模型对目标形变的适应能力，使得网络在面对更复杂的视觉场景时，能够保持更高的准确性和鲁棒性。

这种技术的引入，极大地扩展了卷积神经网络在处理非刚性对象时的能力，为许多计算机视觉任务的改进提供了新的思路。

可变形卷积中的 $\Delta p$ 是通过什么网络得到的？

是的，在可变形卷积（Deformable Convolution）中，生成偏移量 $\Delta p$ 的网络通常是通过一个传统的卷积神经网络得到的。

具体过程如下：

  1. 卷积操作生成偏移量:

    • 在可变形卷积中，首先会对输入特征图（与主要可变形卷积层相同）进行一次标准的卷积操作，这个卷积层专门用于生成偏移量 $\Delta p$。
    • 这个卷积层的卷积核大小通常与后续实际执行可变形卷积的卷积核大小相同。例如，如果可变形卷积的核大小为 $3 \times 3$，那么生成偏移量的卷积层的核大小也是 $3 \times 3$。

  2. 通道数计算:

    • 偏移量 $\Delta p$ 的通道数为 $2 \times \text{kernel size} \times \text{kernel size}$。这是因为每个卷积核位置都需要两个偏移值（一个在 x 方向，一个在 y 方向），而卷积核有 $k \times k$ 个位置。
    • 以 $3 \times 3$ 的卷积核为例，$\Delta p$ 的通道数为 $2 \times 3 \times 3 = 18$。

  3. 使用传统卷积层:

    • 生成 $\Delta p$ 的卷积层是一个传统的卷积层，这意味着它的参数是通过标准的反向传播算法进行训练和优化的。
    • 输入这个卷积层的特征图经过标准卷积操作后，输出的通道数即为上述的 $2 \times k \times k$。

  4. 卷积层的具体作用:

    • 这个卷积层的目的是生成每个位置的偏移量 $\Delta p$，这些偏移量在后续的可变形卷积中用于调整卷积核的位置，使得卷积核能够更好地适应输入图像的几何变形。

例子说明：

假设有一个输入特征图，其通道数为 $C$（例如 64），卷积核大小为 $3 \times 3$。生成偏移量的卷积层接受这个输入特征图，并输出通道数为 18（即 $2 \times 3 \times 3$）的特征图，其中每个像素点包含 18 个值，这 18 个值表示在该位置上 $3 \times 3$ 卷积核的 9 个点的 x 和 y 方向的偏移量。

总结来说，生成 $\Delta p$ 的卷积层确实是一个传统的卷积层，其参数通过训练数据进行学习，并在整个网络中与其他层一起优化。这个卷积层可以看作是一个辅助模块，用于为可变形卷积提供灵活的采样位置。

Refs: Deformable Convolution ｜可变形卷积_哔哩哔哩_bilibili

Label 生成


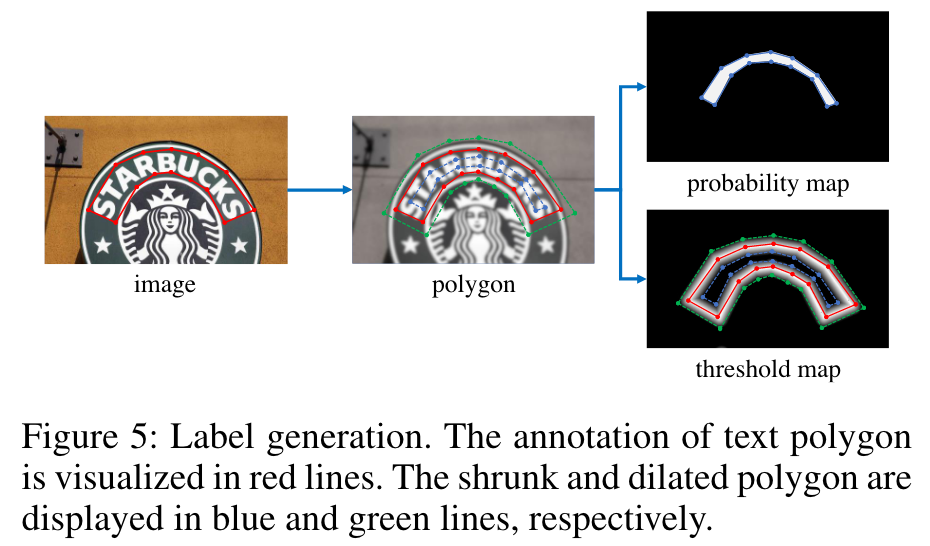
蓝色区域用 Vatti clipping 算法缩放，公式如下，r以经验设为 0.4.

Loss

总损失函数公式及说明

根据您提供的文档中的信息，损失函数 $L$ 可以表示为概率图的损失 $L_s$、二值图的损失 $L_b$、以及阈值图的损失 $L_t$ 的加权和：

其中：

  • $L_s$ 是概率图的损失，通常使用二值交叉熵损失（Binary Cross-Entropy Loss, BCE）。
  • $L_b$ 是二值图的损失，使用的也是二值交叉熵损失。
  • $L_t$ 是阈值图的损失，使用的是 L1 距离（即预测值和标签值之间的绝对差值）的和。

公式中的 $\alpha$ 和 $\beta$ 是两个权重参数，用于调整这三个损失项对总损失的影响。文中建议将 $\alpha$ 设置为 1.0，$\beta$ 设置为 10.0。

损失项的具体公式

  1. 概率图和二值图的损失：

    其中，$y_i$ 是第 $i$ 个像素的标签，$x_i$ 是第 $i$ 个像素的预测值，$S_l$ 是采样的像素集合，通常正负样本的比例为 1:3（难样本挖掘）。

  2. 阈值图的损失：

    为L1 loss. 其中，$y^*_i$ 是第 $i$ 个像素在阈值图中的标签值，$x^*_i$ 是第 $i$ 个像素的预测值，$R_d$ 是扩展后的文本多边形 $G_d$ 内的像素索引集合。

总结

总损失函数 $L$ 由三个部分组成：概率图的损失 $L_s$、二值图的损失 $L_b$ 和阈值图的损失 $L_t$。其中，概率图和二值图的损失项使用的是二值交叉熵损失，这些损失衡量了模型在预测像素属于文本区域或背景时的准确性。而阈值图的损失使用的是 L1 损失，用来优化预测的阈值与真实标签之间的差距。最终的损失函数通过对这三部分损失进行加权求和来得到，总损失函数中的权重参数 $\alpha$ 和 $\beta$ 决定了每个部分在总损失中的影响程度。

交叉熵损失的数值不稳定性

交叉熵损失的数值不稳定性

为了处理数值不稳定的问题，通常会在计算过程中加入一个小的常数 $\epsilon$，使得 $x_i$ 和 $1 - x_i$ 永远不会完全为 0。这样可以避免对数函数的无穷大负值。常见的处理方法是：

对概率值进行剪裁（Clipping）：在计算对数之前，将 $x_i$ 的值限制在一个很小的范围内，例如 $[\epsilon, 1 - \epsilon]$，其中 $\epsilon$ 是一个非常小的常数（如 $10^{-8}$）。这样可以防止对数操作中出现极端的负值。

修改后的交叉熵损失计算公式为：

为什么概率图和二值图不能用 L1 损失？

交叉熵损失_VS_L1Loss
**以DBNet的概率图和二值图用交叉熵损失，阈值图用 L1 loss为例：** 概率图和二值图涉及的是分类任务，因此需要损失函数能够有效地评估和优化模型的分类性能。L1 损失主要用于回归任务，其计算方法和目标不适合处理分类任务中的概率分布问题。
1. 任务性质的不同

  • 概率图：概率图输出的是每个像素属于文本区域的概率值，通常在 [0, 1] 范围内。目标是估计概率分布，表示像素属于文本区域的置信度。这是一个分类任务的输出。

  • 二值图：二值图是概率图经过阈值化处理得到的二分类结果。其目标是将像素分类为文本区域（1）或背景区域（0）。尽管结果是二值的，但其生成过程中依赖于概率图的输出。

  • L1 损失：L1 损失（绝对误差损失）用于回归任务，通过计算预测值与真实值之间的绝对差异来优化模型。在分类任务中，这种损失函数不适合处理概率分布。

2. 交叉熵损失的适用性

  • 分类任务的适应性：交叉熵损失是一种专门用于分类任务的损失函数。它通过计算预测概率分布与真实标签之间的差异来衡量分类性能，适用于处理概率图和二值图。

  • 概率分布的匹配：交叉熵损失能够衡量概率分布之间的距离，它通过优化模型的预测概率分布来提高分类准确性。

3. L1 损失的局限性

  • 不适合分类任务：L1 损失用于回归任务，计算预测值与真实值之间的绝对差异。在分类任务中，尤其是概率分布的处理上，L1 损失不能有效地捕捉概率分布与真实标签之间的差异。

  • 忽视分类错误：即使预测概率值接近真实值，L1 损失只关注预测值与真实值的绝对差异，不能充分反映最终分类决策的准确性。例如，真实标签为 1 时，预测概率为 0.49 的分类可能被误认为是背景区域 0，这种分类错误可能无法通过 L1 损失有效反映。

4. 交叉熵损失的优越性

  • 分类错误的惩罚：交叉熵损失直接处理分类任务，能够显著反映分类错误的严重性。例如，对于真实标签 1 和预测概率值 0.49，交叉熵损失会计算 $-\log(0.49)$，值较大，能够更好地反映分类错误。

  • 优化概率分布：交叉熵损失优化预测概率分布，减少与真实标签之间的差异，适合处理分类任务中的细微差别，从而提高分类的准确性。

总结

L1 损失关注的是预测值与真实值之间的绝对差异，不适合处理分类任务中的概率分布问题。交叉熵损失专门用于分类任务，能够有效地优化概率分布与真实标签之间的差异，从而更好地处理分类任务中的细微差别。

推理阶段

最后的预测结果为概率图或近似二值图，以阈值 0.2进行二值化。
然后仍然以Vatti clipping 算法进行膨胀：

这里 $r’$ 设为 1.5.

为什么推理阶段可以直接用概率图

提供丰富的监督信号：
通过额外的监督信号，是模型学习到，在边界区域不应该预测为像素，模型也会对生成的概率图在边界区域预测为文字进行抑制。