0%

BMN详解

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 4.4k 阅读时长 ≈ 7 分钟

BMN(Boundary-Matching Network) 详解。

Intro

百度，ActivityNet Challenge 2019 冠军模型：BMN: Boundary-Matching Network for Temporal Action Proposal Generation。

Problem Formulation

  1. Unlike temporal action detection task, in the work categories of action instances are not taken into account in proposal generation task.
  2. The temporal annotation: $\Psi_g=\left \{ \varphi_n=(t_{s,n}, t_{e,n}) \right \} ^{N_g}_{n=1}$, here $N_g$ is the amount of ground-truth action instances.
  3. During inference, proposal generation method should generate proposals $\Psi_p$ which cover $\Psi_g$ precisely and exhaustively.

网络结构：


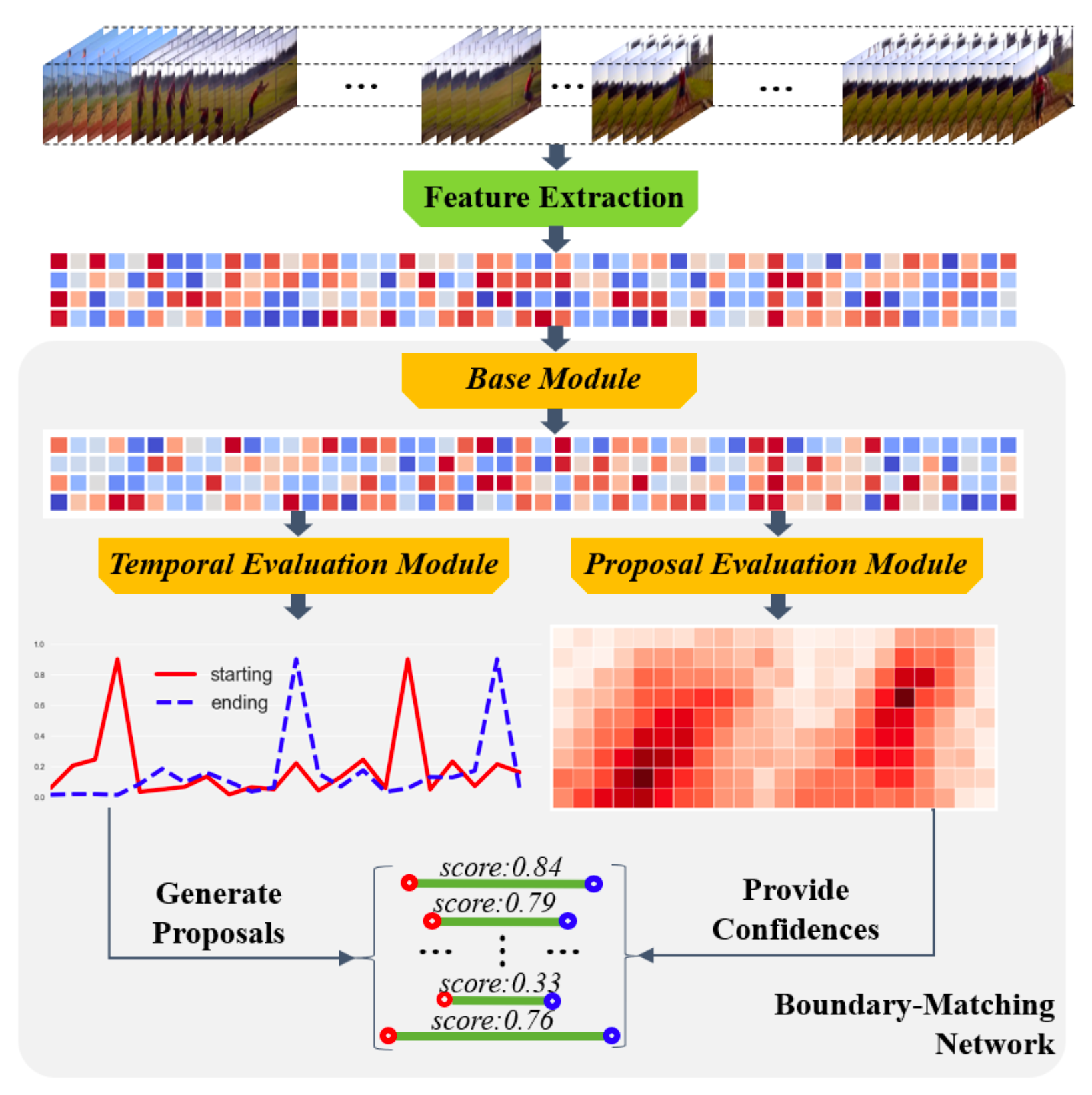
流程

  1. Feature Extraction: 使用双流网络（光流+RGB），获得feature map.
  2. Base Module： 1x1卷积（时序卷积）。
  3. Temporal Evaluation Module(TEM)： 1x1卷积（时序卷积），获得开始、结束点的概率序列。
  4. Proposal Evaluation Module(PEM)：
    1. [[PapersRead#BMN#BM layer|BM layer]]
    2. 通过conv3d, conv2d 得到置信度图。
  5. 生成结果：
    1. 把两条边界概率序列中大于$极大值\times \frac{1}{2}$ 或是峰值（极大值）的都看作开始或结束边界.
    2. $n^2$复杂度两两组合，获得一系列proposals:
    3. 根据置信度图获得各个proposals的置信度。
      1. the proposal denoted: $φ = (t_s, t_e, p^s_{ts} , p^e_{te} , p_{cc}, p_{cr})$
        where $p^s_{ts}, p^e_{te}$ are starting and ending probabilities. $p_{cc}, p_{cr}$ are classification confidence and regression confidence score.
      2. get final score: $p_f = p^s_{ts} · p^e_{te} · \sqrt{p_{cc}· p_{cr})}$
    4. 利用Soft-NMS去冗余。

置信度图：

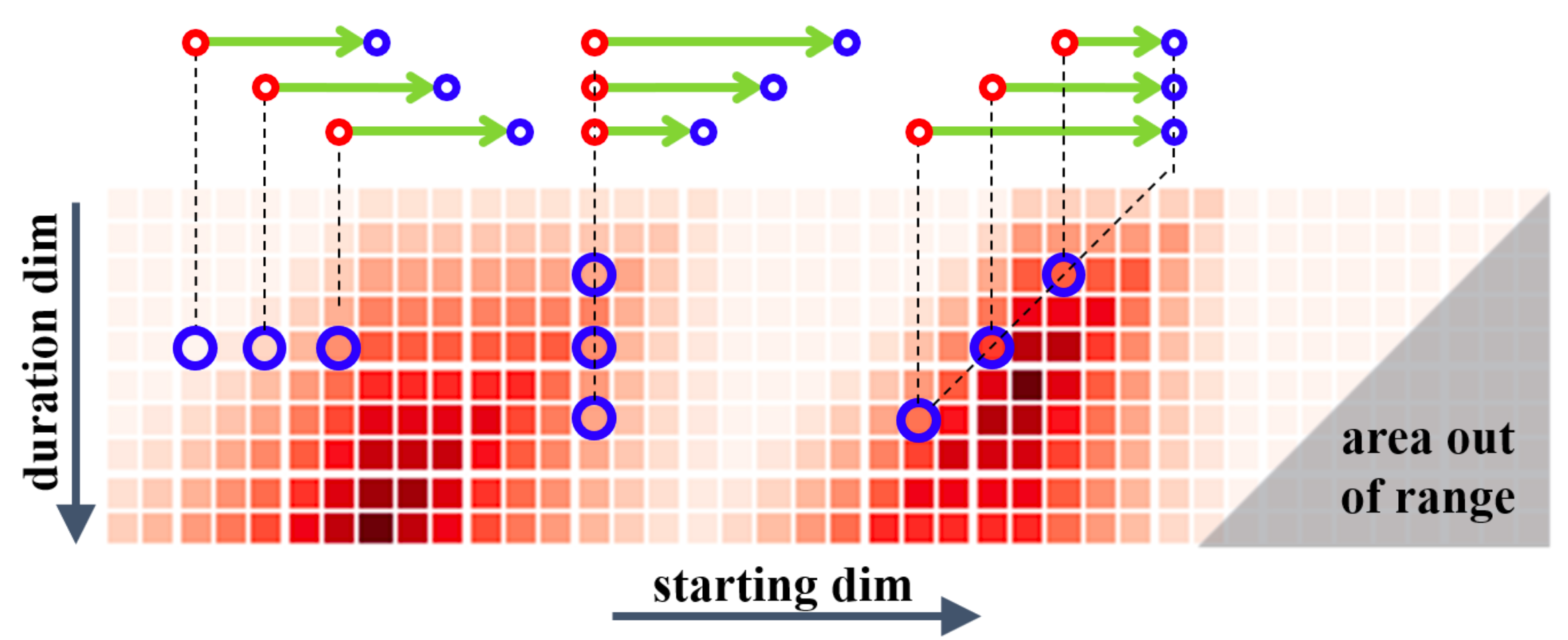
  1. $M_C\in R^{D×T}$.
  2. 由开始点和长度决定结束点，从而确定一个proposal. 所以上图对应所有任意视频段的置信度。
  3. duration dim: proposal长度.
  4. starting dim: 开始点位置。
  5. 同一行对应的proposals对应相同的长度。同一列队对应的proposals拥有相同的开始点。同一负对角线对应的proposals拥有相同的结束边界。右下角部分proposals超出视频范围，无意义。

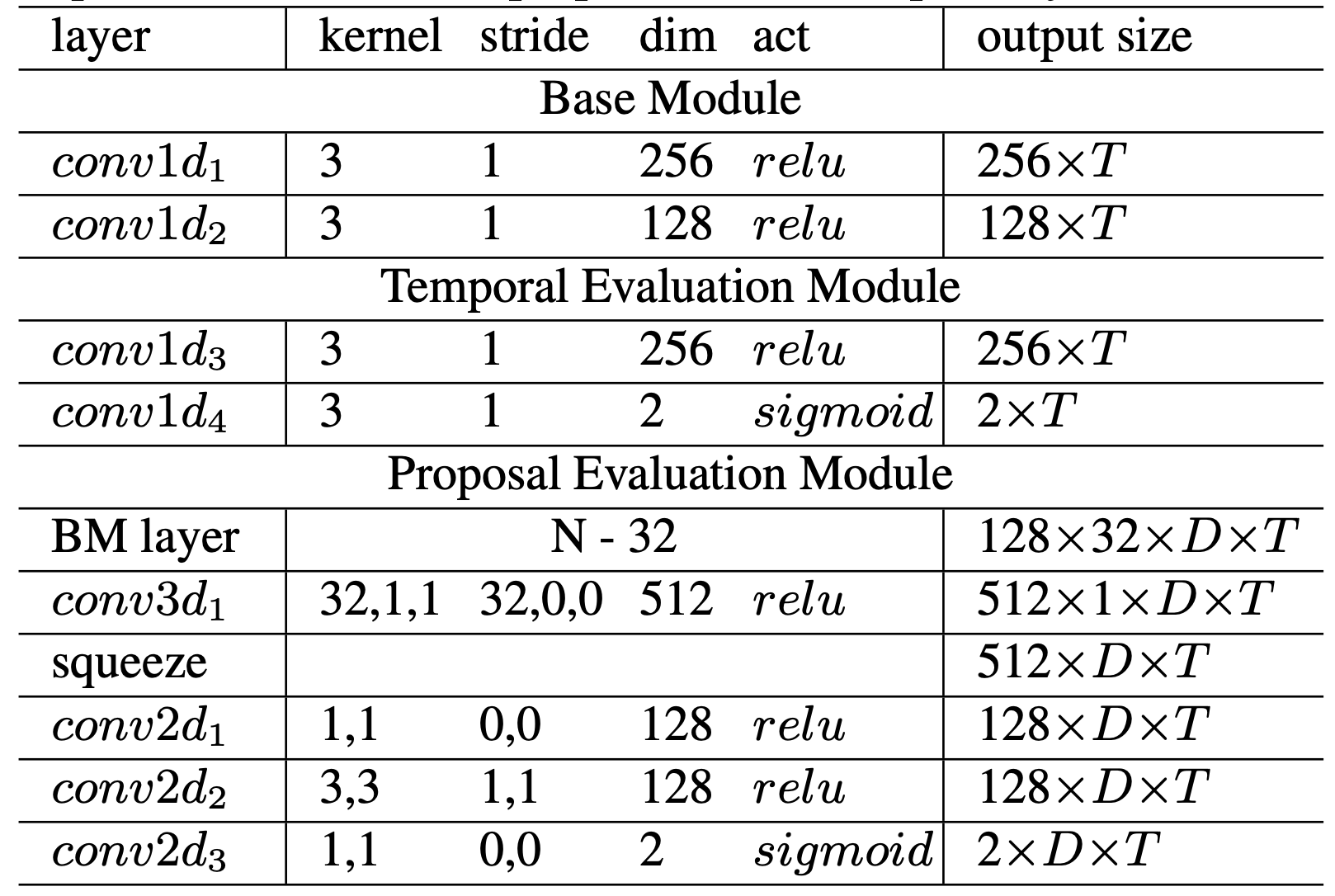
BM layer

  1. The goal: uniformly sample N points in $S_{F} ∈ R^{C×T}$ between starting boundary $t_{s}$ and ending boundary $t_{e}$ of each proposal $φ_{i,j}$, and get proposal feature $m^f_{i,j} ∈ R^{C×N}$ with rich context (actually sampling in [$t_S-0.25d, t_e+0.25d$]).
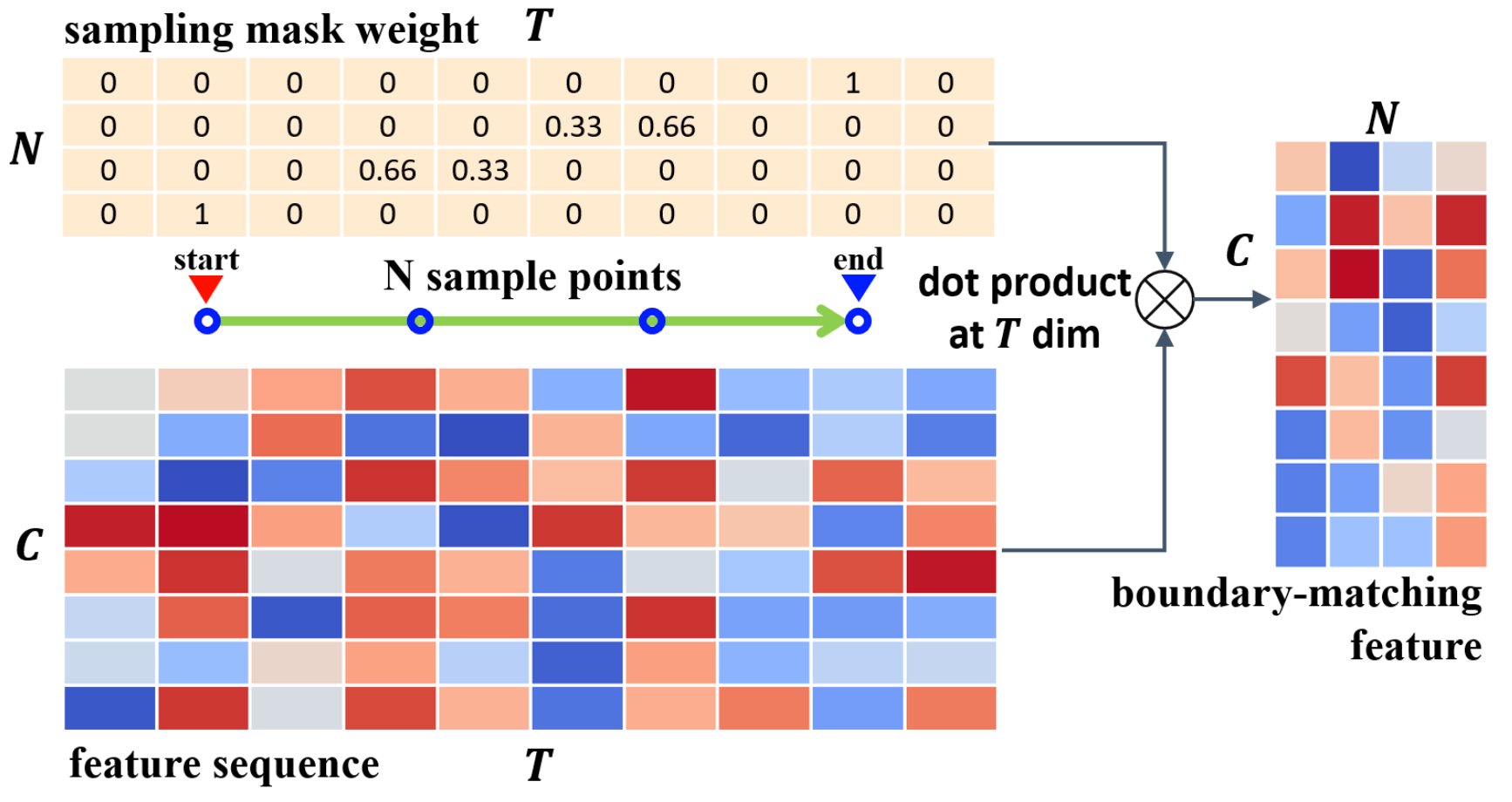
  2. two problems:
    1. how to sample feature in non-integer point:
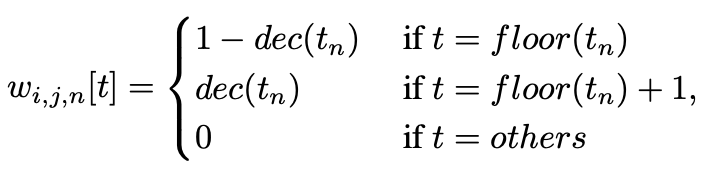
    2. how to sample feature for all proposals simultaneously:
      1. expanding $w_{i,j} ∈ R^{N ×T}$ to $W ∈ R^{N ×T ×D×T}$ for all proposals in BM confidence map.
      2. get $M_F ∈ R^{C×N×D×T}$ by using dot product: $S_{F} ∈ R^{C×T}$ and $W^T ∈ R^{T×N×D×T}$. （$W$ can be pre-generated because it’s the same for different videos, the inference speed of BM layer is very fast. Is T is the same for the different videos? Ans: BMN#Base module|Base module and BMN#Training of BMN#Training Data Construction|Training Data Construction. TODO: review code）

Base module

  1. adopt a long observation window with length $l_ω$ to truncate the untrimmed feature sequence with length $l_f$ .
  2. So here $l_w$ is $T$ in $S_{F} ∈ R^{C×T}$.

Proposal Evaluation Module(PEM)

  1. Final generate: $M_C\in R^{D×T}$, but there are two predicted $M_C$: $M_{CC}$, $M_{CR}$, being trained using binary classification and regression loss function separately. TODO: review code.

Training of BMN

TEM vs PEM:

  1. TEM: learns local boundary.
  2. PEM: pattern global proposal context.

Training Data Construction:

  1. firstly, extract all feature sequence F with length.
  2. get many observation windows with length $l_w$ with 50% overlap.
  3. here every window contains at least one ground-truth action instance.

Label Assignment

TEM

  1. denote its starting and ending regions as $r_S = [t_s − d_g /10, t_s +d_g/10]$ and $r_E =[t_e−d_g/10,t_e+d_g/10]$separately.
  2. denote its local region as $r_{t_n} = [t_n −d_f /2, t_n +d_f /2]$, where $d_f = t_n −t_{n−1}$ is the temporal interval between two locations.
  3. Then calculate overlap ratio IoR of $r_{t_n}$ with $r_S$ and $r_E$ separately, and denote maximum IoR as $g^s_{t_n}$ and $g^e_{t_n}$ separately.
  4. here IoR is defined as the overlap ratio with ground-truth proportional to the duration of this region. TODO: code review.
  5. Thus generate $G_{S,ω}=\{g^s_{t_n}\}^{l_w}_{n=1}$ and $G_{E,ω}=\{g^e_{t_n}\}^{l_w}_{n=1}$ as label of TEM.

PEM

  1. Purpose: BM label map $G_C ∈ R^{D×T}$.
  2. For a proposal $φ_{i,j}=(t_s=t_j, t_e=t_j+t_i)$ , calculate its IoU with all $φ_g$ in $Ψ_ω$, and denote the maximum IoU as $g^c_{i,j}$ . Thus we can generate $G_C=\{g^c_{i,j}\}^{D,l_ω}_{i,j=1}$ as label of PEM.

Loss

Loss of TEM

  1. adopt weighted binary logistic regression loss function $L_{bl}$, to get the sum of starting and ending losses:
  2. $L_{bl}(P,G)$:
    $\frac{1}{l_w}\sum_{i=1}^{l_w}(a^+·b_i·log(p_i)+a^-·(1-b_i)·log(1-p_i))$
    where $b_i = sign(g_i − θ)$ is a two-value function used to convert $g_i$ from [0, 1] to {0, 1}0, 1} based on overlap threshold$θ = 0.5$. Denoting $l^+=\sum b_i$ and $l^− = l_ω −l^+$, the weighted terms are $α^+ = \frac{l_w}{l^+}$ and $α^- = \frac{l_w}{l^-}$.

Loss of PEM

  1. Define:
    $L_{PEM} =L_C(M_{CC},G_C)+λ·L_R(M_{CR},G_C)$
    1. here $L_{bl}$ for $L_C$ , L2 loss for $L_R$ . $λ = 10$ .
    2. to balance the ratio between positive and negative samples in $L_R$ , take all points with $g^C_{i,j}>0.6$ as positive, and randomly sample $g^C_{i,j}<0.2$ as negative, ensure 1:1 for positive: negative.

Training Objective

$L=L_{LEM} +λ_1 ·L_{GEM} +λ_2 ·L_2(Θ)$
where $L_2(Θ)$ is L2 regularization term, $λ_1$, $λ_2$ are set to 1, 0.000 to ensure different modules are trained evenly.

Refs:

  1. https://zhuanlan.zhihu.com/p/337432552
  2. https://arxiv.org/pdf/1907.09702.pdf